Подпространства (ru)

2025-07-03

math

Начнём с полезного определения: Ненулевые векторы $u, v \in \mathbb{R}$ называются коллинеарными векторами, если они пропорциональны друг другу, то есть существует $\lambda \in \mathbb{R}$ такое, что $u = \lambda v$. Коллинеарные векторы обозначаются как $u || v$. Нулевой вектор коллинеарен любому вектору. Геометрически векторы коллинеарны, если они имеют одинаковое или противоположное направление.

Рассмотрим плоскость $\pi$ в пространстве $\mathbb{R}^3$, проходящую через начало координат. Возьмём два неколлинеарных вектора $u$ и $v$ из этой плоскости. Тогда любую точку $x \in \pi$ можно представить как: $x = \alpha u + \beta v$.

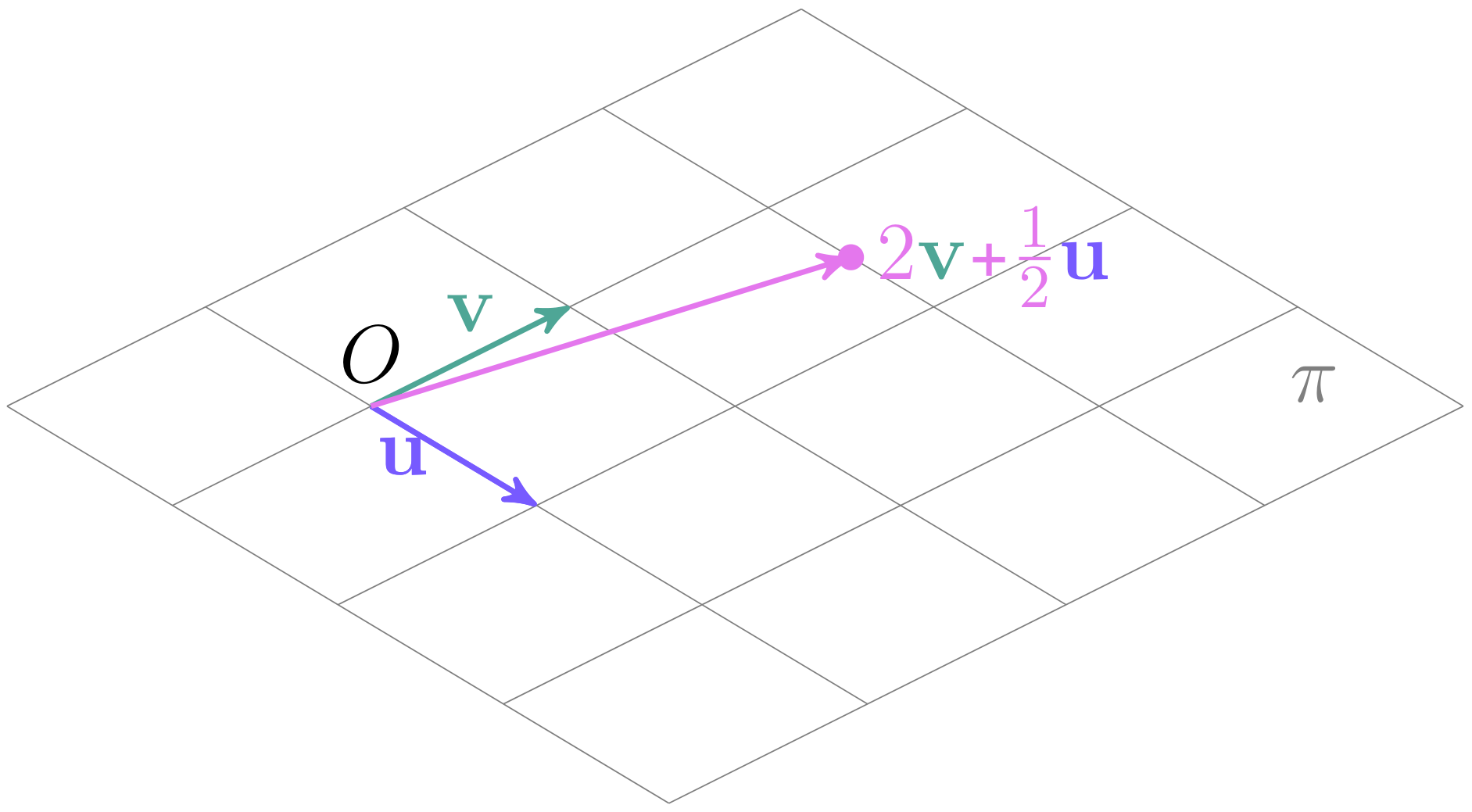Хорошо, это означает, что мы можем определить плоскость $\pi$ как:

Обобщим понятие плоскости, проходящей через начало координат, на пространство произвольной размерности: Линейной оболочкой векторов $v_1, v_2, \dots, v_k \ \in \ \mathbb{R}^n$ называется множество векторов, представимых в виде суммы векторов $v_1, v_2, \dots, v_k$ с произвольными коэффициентами:

Выражение $\alpha_1 v_1 + \alpha_2 v_2 + \dots + \alpha_k v_k$ будем называть линейной комбинацией векторов $v_1, v_2, \dots, v_k$.

Сформулируем ключевое определение: линейным подпространством $\mathbb{R}^n$ называется линейная оболочка конечного числа векторов $v_1, v_2, \dots v_k \ \in \mathbb{R}^n$:

Понятия линейной оболочки и линейного подпространства эквивалентны. Любая линейная оболочка и любое подпространство содержат $0$, поскольку мы можем положить все коэффициенты $\alpha_1, \alpha_2, \dots, \alpha_k$ равными нулю.

Почему линейные подпространства важны? Вот пример:

Возьмём чёрно-белое цифровое фото размером 512 на 512 пикселей. В памяти компьютера это фото может быть представлено как $512 \times 512 = 262144$ чисел — каждое представляет интенсивность соответствующего пикселя от 0 (полностью чёрный) до 1 (полностью белый). Таким образом, фото может быть представлено вектором $x$ в пространстве размерности $d=262144$.

Теперь рассмотрим важную практическую задачу — сжатие фото без значительных потерь. Оказывается, эту проблему можно решить, найдя специальное низкоразмерное подпространство и спроецировав вектор $x$ на это подпространство.

Мы говорили, что подпространство должно содержать ноль. Это означает, что прямая $y = 2x$ является подпространством, а прямая $y = x + 2$ — нет. Но многие свойства подпространств сохраняются, даже когда они не содержат ноль. Такие подпространства называются аффинными подпространствами. Аффинным подпространством $\mathbb{R}^n$ называется множество векторов $A$ вида $a + v$, где $a \in \mathbb{R}^n$ — фиксированный вектор, а вектор $v$ принадлежит линейному подпространству $V$. Пусть линейное подпространство $V$ — это линейная оболочка векторов $v_1, v_2, \dots, v_k$. Тогда аффинное подпространство — это множество:

Пусть $V$ — подпространство в $\mathbb{R}^n$. Размерностью этого подпространства называется минимальное количество векторов $v_1, v_2, \dots, v_k \in \mathbb{R}^n$, необходимых для определения подпространства $V$:

Размерность обозначается как: $\dim{(V)}$. Подумаем об этом. Например, у нас есть два неколлинеарных вектора $u, v \in \mathbb{R}^{100}$ и подпространство $V = \text{span}(u, v)$. Мы знаем, что каждый вектор $x \in V$ имеет 100 координат, но по определению подпространства: $x = \alpha u + \beta v$. Это означает, что любой вектор $x$ определяется всего двумя параметрами $\alpha$ и $\beta$, следовательно $\dim{(V)} = 2$. Для определения точки в $\mathbb{R}^n$ нам нужно $n$ параметров, для определения точки в $V$ нам нужно $\dim{(V)}$ параметров.

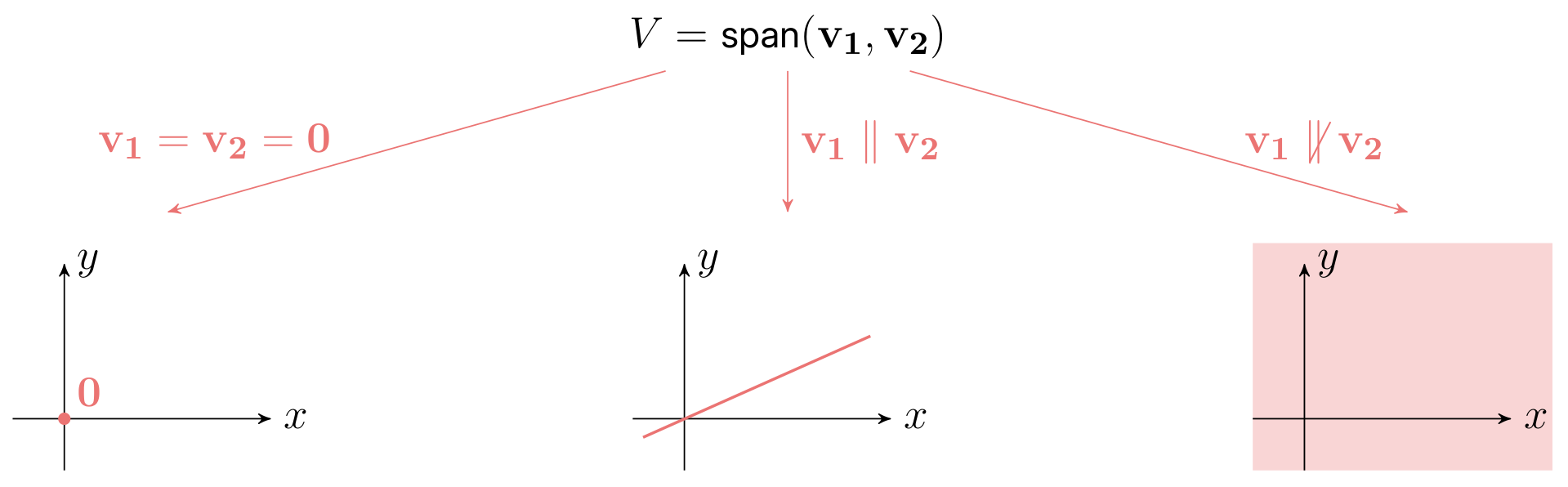
Существует подпространство, определяемое только одним вектором $0$: $V = \text{span}(0)$. Мы называем это подпространство тривиальным и считаем $\dim{(V)} = 0$.

Если у нас есть подпространство $V = \text{span}(v_1, v_2, \dots, v_k)$, может ли $\dim{(V)}$ быть меньше $k$? Да, если и только если один из векторов может быть выражен как линейная комбинация остальных векторов, например: $v_1 = \gamma_2v_2 + \gamma_3v_3 + \dots + \gamma_kv_k$.

Набор векторов называется линейно независимым, если равенство:

выполняется только при $\alpha_1 = \alpha_2 = \dots = \alpha_k = 0$. Если равенство может выполняться при ненулевых коэффициентах, векторы линейно зависимы.

Рассмотрим пространство $\mathbb{R}^n$ и заданный ненулевой вектор $w \in \mathbb{R}^n$. Тогда множество векторов $P$, перпендикулярных $w$:

является линейным подпространством с $\dim{(P)} = n - 1$