Основы многомерных векторов (ru)

2025-06-26

math

Что такое вектор? Для натурального числа $n$ назовём вектором упорядоченный список из $n$ действительных чисел $v = \begin{pmatrix}v_1&v_2&v_3&\ldots&v_n\end{pmatrix}$. Число $n$ называется размерностью вектора: $\dim{v} = n$. Множество всех возможных векторов размерности $n$ обозначается $R^n$. Обычные числа называются “скалярами”. Например, $5$ — скаляр, а $\begin{pmatrix}1&3\end{pmatrix}$ — вектор.

Базовые операции с векторами

1. Сумма векторов — сумма соответствующих координат: $$ v + w = \begin{pmatrix}v_1 \\ v_2 \\ \ldots \\ v_n \end{pmatrix} + \begin{pmatrix}w_1 \\ w_2 \\ \ldots \\ w_n \end{pmatrix} = \begin{pmatrix}v_1 + w_1 \\ v_2 + w_2 \\ \ldots \\ v_n + w_n \end{pmatrix} $$ Складывать можно только векторы одинаковой размерности.
2. Умножение вектора на скаляр: $$ \lambda v = \lambda \cdot \begin{pmatrix}v_1 \\ v_2 \\ \ldots \\ v_n \end{pmatrix} = \begin{pmatrix}\lambda v_1 \\ \lambda v_2 \\ \ldots \\ \lambda v_n \end{pmatrix} $$
3. Разность векторов — сумма векторов, где один умножен на скаляр $-1$.
4. Скалярное произведение векторов: $$ x \cdot y = \langle x;y\rangle = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n = \sum \limits_{i = 1}^{n}x_i y_i $$ Свойства скалярного произведения:

• Коммутативность: $\langle v; w\rangle = \langle w; v\rangle$
• Дистрибутивность: $\langle x; (v + w)\rangle = \langle x; v\rangle + \langle x; w \rangle$
• Совместимость со скалярным умножением: $\langle v; \lambda w\rangle = \lambda \langle v;w\rangle$
• Если скалярное произведение равно нулю, векторы называются ортогональными

Геометрическая интерпретация

В геометрии вектор — направленный отрезок.

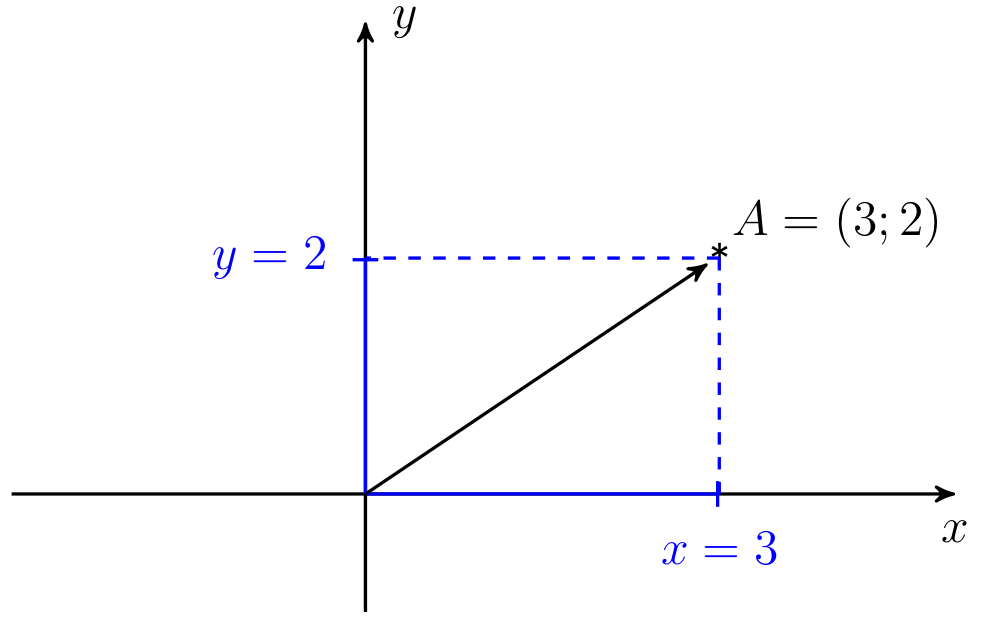
Длина вектора вычисляется по теореме Пифагора: ФОРМУЛА_4. Вектор единичной длины называется единичным вектором. Ненормированный вектор можно нормировать умножением на $\lambda = \frac{1}{||v||}$. Расстояние между векторами: $d = ||v - w|| = \sqrt{\sum\limits_{i = 1}^{n}{(v_i - w_i)^2}}$ Угол между векторами:

Проекция вектора $u$ на $w$:

Неравенство Коши-Буняковского:

Неравенство треугольника: $||v + w|| \leqslant ||v|| + ||w||$
Для ортогональных векторов выполняется теорема Пифагора: $||a + b||^2 = ||a||^2 + ||b||^2$.```