Subsapces (en)

2025-07-03

math

Start with useful definition: Non-zero vectors $u, v \in \mathbb{R}$ call collinear vectors, if they are proportional to each other, that is exist $\lambda \in \mathbb{R}$, that $u = \lambda v$. Collinear vectors denoted as $u || v$. Zero-vector collinear with any vector. Geometrically, vectors collinear, if they have same or opposite direction.

Let’s consider the plane $\pi$ in $\mathbb{R}^3$ space, which passes through zero-coordinate. Consider two non-collinear vectors $u$ an $v$ from this plane. Then, any point $x \in \pi$ we can be represented as: $x = \alpha u + \beta v$.

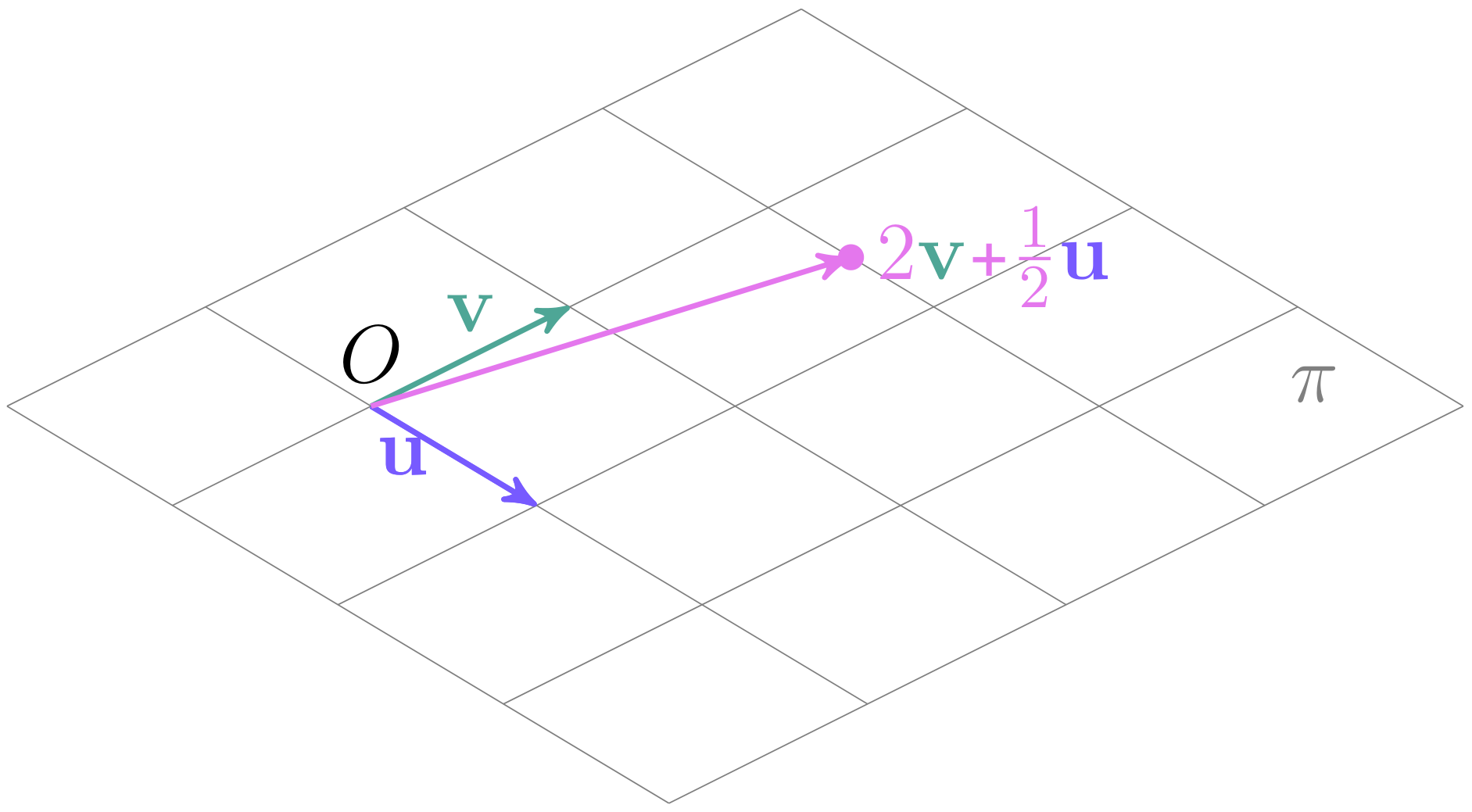Okay, it’s mean we can define plane $\pi$ as:

Let’s generalize the concept of a plane passing through the origin to a space of arbitrary dimension: The linear Span of vectors $v_1, v_2, \dots, v_k \ \in \ \mathbb{R}^n$ is called set of vectors, represented in form of sum of vectors $v_1, v_2, \dots, v_k$ with arbitrary ratio:

Expression $\alpha_1 v_1 + \alpha_2 v_2 + \dots + \alpha_k v_k$ will call linear combination of vectors $v_1, v_2, \dots, v_k$.

Let’s final this with pivotal definition: linear subspace $\mathbb{R}^n$ called span of finite numbers of vectors $v_1, v_2, \dots v_k \ \in \mathbb{R}^n$:

The span concept and subspace concept equivalents. And any span and subspace contain a $0$, because we can make all ratio $\alpha_1, \alpha_2, \dots, \alpha_k$ equal to zero .

Why linear subspace is important? Here is an example:

Let us take a black-and-white digital photograph of size 512 by 512 pixels. In computer memory, this photograph can be represented as $512 \times 512 = 262144$ numbers — each representing the intensity of the corresponding pixel, ranging from 0 (completely black) to 1 (completely white). Thus, the photograph can be represented as a vector $x$ in a space of dimension $d=262144$.

Now, let us consider an important practical problem — compressing the photograph without significant loss. It turns out that this problem can be solved by finding a special low-dimensional subspace and projecting the vector $x$ onto this subspace.

We told, that subspace need to contain zero. It’s mean line $y = 2x$ is a subspace, but line $y = x + 2$ not. But many properties of subspace saved when it doesn’t contain zero. Therefore, we call such subspaces as affine subspaces. Affine subspaces of $\mathbb{R}^n$ is a set of vectors $A$ of the form $a + v$, where $a \in \mathbb{R}^n$ — is a fixed vector, and vector $v$ belongs to linear subspace $V$. Let linear subspace $V$ is span of vectors $v_1, v_2, \dots, v_k$. Then, affine affine subspace is a set:

Let $V$ — subspace in $\mathbb{R}^n$. Dimension of this subspace is minimal count of vectors $v_1, v_2, \dots, v_k \in \mathbb{R}^n$ for define subspace $V$:

Dimension is denoted by: $\dim{(V)}$. Let’s think about it. For example, we have two non-collinear vectors $u, v \in \mathbb{R}^{100}$ and subspace $V = \text{span}(u, v)$. We know every vector $x \in V$ have 100 coordinates, but, by subspace definition: $x = \alpha u + \beta v$. it’s mean any vector $x$ defined only two parameters $\alpha$ and $\beta$, therefore $\dim{(V))} = 2$. For define point in $\mathbb{R}^n$ we need $n$ parameters, for define point in $V$ we need $\dim{(V)}$ parameters.

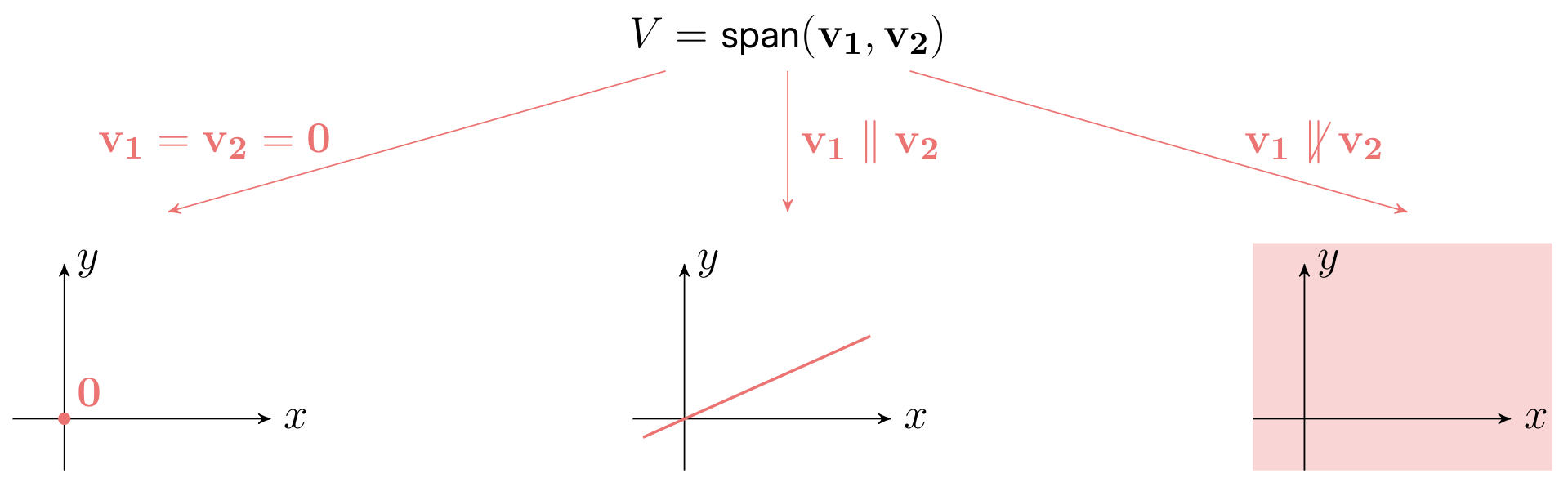
Exist subspace, which defined only one vector $0$: $V = \text{span}(0)$. We call this subspace trivial, and considered $\dim{(V)} = 0$.

If we have subspace $V = \text{span}(v_1, v_2, \dots, v_k)$, when $\dim{(V)}$ can be smaller than $k$? if and only if one of the vectors can be express as linear combination rest vectors, for example: $v_1 = \gamma_2v_2 + \gamma_3v_3 + \dots + \gamma_kv_k$.

Set of vectors called linearly independent if equality:

holds only for $\alpha_1 = \alpha_2 = \dots = \alpha_k = 0$. If equality can be holds for non-zero rates, vectors linearly dependent.

Consider space $\mathbb{R}^n$ and a given non-zero vector $w \in \mathbb{R}^n$ . Then set of vectors $P$, perpendicular $w$:

is linear subspace with $\dim{(P)} = n - 1$